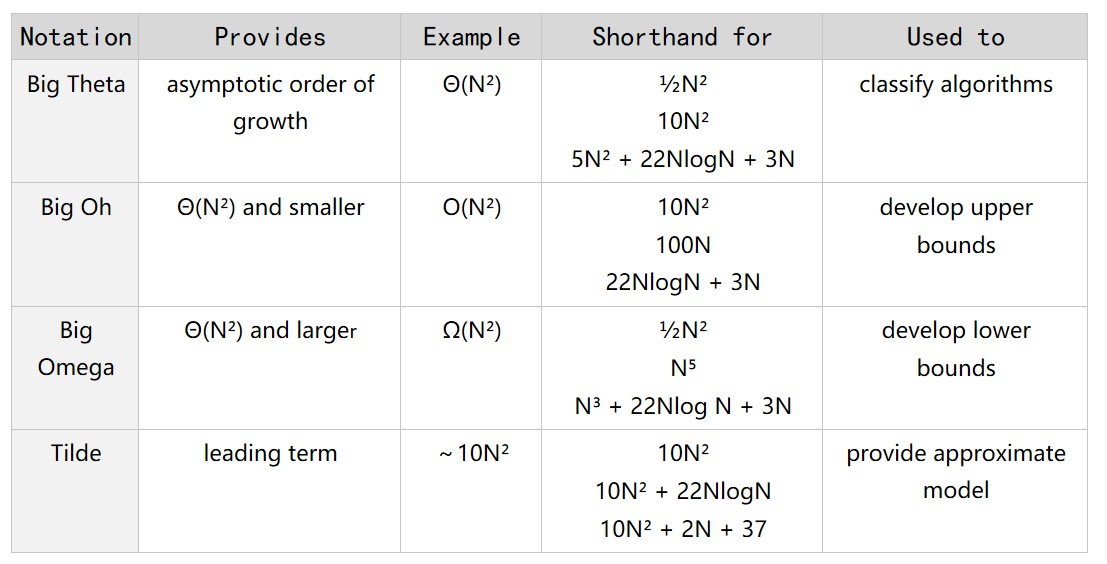
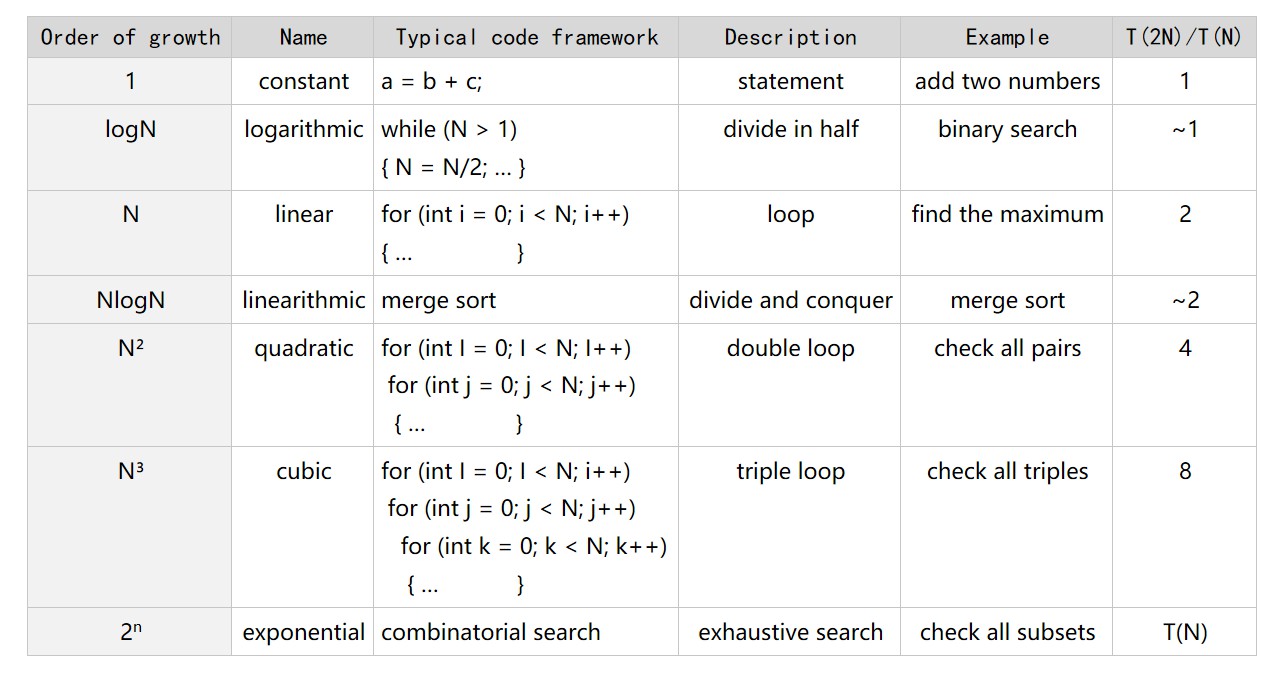
距上次写博有一个多月了,偷懒了……
Coursera上算法四的课程第一周讲的是union-find算法和算法分析的基础,通过开发、改进union-find算法的过程,解剖麻雀,向我们展示开发算法的一般过程。
Union-find算法
UF是一种树型的数据结构,常常用来处理一些不相交的集合。这部分课程一开始讨论设计API,之后的内容围绕开发设计的API展开,从最初的实现一步步改良,逐步达到理想要求。UF类定义了四个用于此数据结构的操作,union、find、connected、count。以下是不断改良的路径压缩的加权quick-union算法(WQUPC)实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| public class UF {
private int[] id;
private int[] size;
private int count;
public UF(int N) {
count = N;
id = new int[N];
size = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
size[i] = 1;
}
}
public int count() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public int find(int p) {
while (p != id[p]) {
id[p] = id[id[p]];
p = id[p];
}
return p;
}
public void union(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) {
return ;
}
if (size[pID] > size[qID]) {
id[qID] = pID;
size[pID] += size[qID];
} else {
id[pID] = qID;
size[qID] += size[pID];
}
count--;
}
public static void main(String[] args) {
int N = StdIn.readInt();
UF uf = new UF(N);
while (!StdIn.isEmpty()) {
int p = StdIn.readInt();
int q = StdIn.readInt();
if (uf.connected(p, q))
continue;
uf.union(p, q);
StdOut.println(p + " " + q);
}
StdOut.println(uf.count() + " components");
}
}
|
数据结构UF的亮点是仅仅维护两个数组,一个用于维护父节点,一个用于维护权重,两个数组经过如此包装,优雅转身变成一个高级的数据结构。这个实现中还使用了路径压缩的方法,其实就是一行代码,id[i] = id[id[i]],将父节点更新为祖父节点。WQUPC的union操作和find操作在均摊成本下非常接近1,已是最优的实现了。
此周的作业是数据结构UF在渗滤(percolation)模型中的应用,运行代码跑出图形界面的那一刻,眼睛一亮,非常有意思。
算法分析基础
学习算法当然是为了让程序短小精悍,优雅地编码。这部分围绕3-sum问题展开,增长数量级为平方级别的是不行的,我们追求的是线性对数级别或线性级别的及其以下的算法。